Khan Academy on a Stick
Solid of revolution
Using definite integrals with the shell and disc methods to find volumes of solids of revolution.
-
 Disk method around x-axis
Disk method around x-axis
Finding the solid of revolution (constructed by revolving around the x-axis) using the disc method.
-
 Generalizing disc method around x-axis
cc
Generalizing disc method around x-axis
ccGeneralizing what we did in the last video for f(x) to get the "formula" for using the disc method around the x-axis
-
 Disc method around y-axis
Disc method around y-axis
Finding the volume of a figure that is rotated around the y-axis using the disc method
-
 Disc method (washer method) for rotation around x-axis
Disc method (washer method) for rotation around x-axis
Finding the volume of a solid of revolution that is defined between two functions
-
 Generalizing the washer method
Generalizing the washer method
Looking at the example from the last video in a more generalized way
-
 Disc method rotation around horizontal line
Disc method rotation around horizontal line
Solid of revolution constructing by rotating around line that is not an axis
-
 Washer method rotating around non-axis
Washer method rotating around non-axis
Washer method when rotating around a horizontal line that is not the x-axis
-
 Part 2 of washer for non axis rotation
Part 2 of washer for non axis rotation
Doing some hairy algebra and arithmetic to evaluate the definite integral from the last video
-
 Disc method rotating around vertical line
Disc method rotating around vertical line
Volume of solid created by rotating around vertical line that is not the y-axis using the disc method.
-
 Calculating integral disc method around vertical line
Calculating integral disc method around vertical line
Let's calculate the integral from the last video.
-
 Washer or ring method for vertical line rotation
Washer or ring method for vertical line rotation
Setting up the definite integral for the volume of a solid of revolution around a vertical line using the "washer" or "ring" method.
-
 Evaluating integral for washer method around vertical line
Evaluating integral for washer method around vertical line
Evaluating integral set up in the last video using washer method.
Disc method
You know how to use definite integrals to find areas under curves. We now take that idea for "spin" by thinking about the volumes of things created when you rotate functions around various lines. This tutorial focuses on the "disc method" and the "washer method" for these types of problems.
-
 Shell method for rotating around vertical line
Shell method for rotating around vertical line
Introducing the shell method for rotation around a vertical line.
-
 Evaluating integral for shell method example
Evaluating integral for shell method example
Evaluating the definite integral set up using the shell method
-
 Shell method for rotating around horizontal line
Shell method for rotating around horizontal line
Example showing how to find the volume of a solid of revolution (constructed by rotating around the x-axis) using the shell method (this could have been done with the disk method as well).
-
 Shell method with two functions of x
Shell method with two functions of x
Using the shell method to rotate around a vertical line.
-
 Calculating integral with shell method
Calculating integral with shell method
Evaluating integral set up with shell method for two functions.
-
 Shell method with two functions of y
Shell method with two functions of y
-
 Part 2 of shell method with 2 functions of y
Part 2 of shell method with 2 functions of y
Shell method
You want to rotate a function around a vertical line, but do all your integrating in terms of x and f(x), then the shell method is your new friend. It is similarly fantastic when you want to rotate around a horizontal line but integrate in terms of y.
-
 Disc method: function rotated about x-axis
cc
Disc method: function rotated about x-axis
ccFiguring out the volume of a function rotated about the x-axis.
-
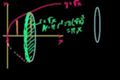 Disc method (rotating f(x) about x axis)
cc
Disc method (rotating f(x) about x axis)
ccThe volume of y=sqrt(x) between x=0 and x=1 rotated around x-axis
-
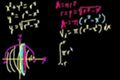 Volume of a sphere
cc
Volume of a sphere
ccFiguring out the equation for the volume of a sphere.
-
 Disc method with outer and inner function boundaries
cc
Disc method with outer and inner function boundaries
ccMore volumes around the x-axis.
-
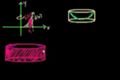 Shell method to rotate around y-axis
cc
Shell method to rotate around y-axis
ccUse the "shell method" to rotate about the y-axis
-
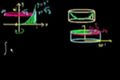 Disk method: rotating x=f(y) around the y-axis
cc
Disk method: rotating x=f(y) around the y-axis
ccUsing the disk method around the y-axis.
-
 Shell method around a non-axis line
cc
Shell method around a non-axis line
ccTaking the revolution around something other than one of the axes.
-
 Shell method around a non-axis line 2
cc
Shell method around a non-axis line 2
ccThe last part of the problem in part 7
Solid of revolution volume
Using definite integration, we know how to find the area under a curve. But what about the volume of the 3-D shape generated by rotating a section of the curve about one of the axes (or any horizontal or vertical line for that matter). This in an older tutorial that is now covered in other tutorials. This tutorial will give you a powerful tool and stretch your powers of 3-D visualization!