Khan Academy on a Stick
Taking derivatives
Calculating derivatives. Power rule. Product and quotient rules. Chain Rule. Implicit differentiation. Derivatives of common functions.
-
 Newton Leibniz and Usain Bolt
cc
Newton Leibniz and Usain Bolt
ccWhy we study differential calculus
Introduction to differential calculus
The topic that is now known as "calculus" was really called "the calculus of differentials" when first devised by Newton (and Leibniz) roughly four hundred years ago. To Newton, differentials were infinitely small "changes" in numbers that previous mathematics didn't know what to do with. Think this has no relevence to you? Well how would you figure out how fast something is going *right* at this moment (you'd have to figure out the very, very small change in distance over an infinitely small change in time)? This tutorial gives a gentle introduction to the world of Newton and Leibniz.
Using secant line slopes to approximate tangent slope
The idea of slope is fairly straightforward-- (change in vertical) over (change in horizontal). But how do we measure this if the (change in horizontal) is zero (which would be the case when finding the slope of the tangent line. In this tutorial, we'll approximate this by finding the slopes of secant lines.
-
 Derivative as slope of a tangent line
cc
Derivative as slope of a tangent line
ccUnderstanding that the derivative is just the slope of a curve at a point (or the slope of the tangent line)
-
 Tangent slope as limiting value of secant slope example 1
Tangent slope as limiting value of secant slope example 1
-
 Tangent slope as limiting value of secant slope example 2
Tangent slope as limiting value of secant slope example 2
-
 Tangent slope as limiting value of secant slope example 3
Tangent slope as limiting value of secant slope example 3
-
 Calculating slope of tangent line using derivative definition
cc
Calculating slope of tangent line using derivative definition
ccCalculus-Derivative: Finding the slope (or derivative) of a curve at a particular point.
-
 The derivative of f(x)=x^2 for any x
cc
The derivative of f(x)=x^2 for any x
ccCalculus-Derivative: Finding the derivative of y=x^2
-
 Formal and alternate form of the derivative
cc
Formal and alternate form of the derivative
cc -
 Formal and alternate form of the derivative example 1
Formal and alternate form of the derivative example 1
-
 Calculus: Derivatives 1
cc
Calculus: Derivatives 1
ccFinding the slope of a tangent line to a curve (the derivative). Introduction to Calculus.
-
 Calculus: Derivatives 2
cc
Calculus: Derivatives 2
ccMore intuition of what a derivative is. Using the derivative to find the slope at any point along f(x)=x^2
Introduction to derivatives
Discover what magic we can derive when we take a derivative, which is the slope of the tangent line at any point on a curve.
Visualizing derivatives
You understand that a derivative can be viewed as the slope of the tangent line at a point or the instantaneous rate of change of a function with respect to x. This tutorial will deepen your ability to visualize and conceptualize derivatives through videos and exercises. We think you'll find this tutorial incredibly fun and satisfying (seriously).
-
 Power Rule
cc
Power Rule
cc -
 Is the power rule reasonable
cc
Is the power rule reasonable
cc -
 Derivative properties and polynomial derivatives
Derivative properties and polynomial derivatives
-
 Proof: d/dx(x^n)
cc
Proof: d/dx(x^n)
ccProof that d/dx(x^n) = n*x^(n-1)
-
 Proof: d/dx(sqrt(x))
cc
Proof: d/dx(sqrt(x))
ccProof that d/dx (x^.5) = .5x^(-.5)
-
 Power rule introduction
cc
Power rule introduction
ccDetermining the derivatives of simple polynomials.
Power rule
Calculus is about to seem strangely straight forward. You've spent some time using the definition of a derivative to find the slope at a point. In this tutorial, we'll derive and apply the derivative for any term in a polynomial. By the end of this tutorial, you'll have the power to take the derivative of any polynomial like it's second nature!
-
 Derivatives of sin x, cos x, tan x, e^x and ln x
Derivatives of sin x, cos x, tan x, e^x and ln x
-
 Chain rule introduction
Chain rule introduction
-
 Chain rule definition and example
Chain rule definition and example
-
 Chain rule with triple composition
cc
Chain rule with triple composition
cc -
 Chain rule for derivative of 2^x
Chain rule for derivative of 2^x
-
 Derivative of log with arbitrary base
Derivative of log with arbitrary base
-
 Extreme Derivative Word Problem (advanced)
cc
Extreme Derivative Word Problem (advanced)
ccA difficult but interesting derivative word problem
-
 The Chain Rule
cc
The Chain Rule
ccPart 4 of derivatives. Introduction to the chain rule.
-
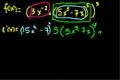 Chain Rule Examples
cc
Chain Rule Examples
ccExamples using the Chain Rule
-
 Even More Chain Rule
cc
Even More Chain Rule
ccEven more examples using the chain rule.
-
 More examples using multiple rules
cc
More examples using multiple rules
ccMore examples of taking derivatives
Chain rule
You can take the derivatives of f(x) and g(x), but what about f(g(x)) or g(f(x))? The chain rule gives us this ability. Because most complex and hairy functions can be thought of the composition of several simpler ones (ones that you can find derivatives of), you'll be able to take the derivative of almost any function after this tutorial. Just imagine.
-
 Derivatives of sin x, cos x, tan x, e^x and ln x
Derivatives of sin x, cos x, tan x, e^x and ln x
-
 Applying the product rule for derivatives
Applying the product rule for derivatives
-
 Product rule for more than two functions
Product rule for more than two functions
-
 Quotient rule from product rule
Quotient rule from product rule
-
 Quotient rule for derivative of tan x
Quotient rule for derivative of tan x
-
 Using the product rule and the chain rule
cc
Using the product rule and the chain rule
cc -
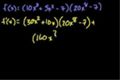 Product Rule
cc
Product Rule
ccThe product rule. Examples using the Product and Chain rules.
-
 Quotient rule and common derivatives
cc
Quotient rule and common derivatives
ccWhy the quotient rule is the same thing as the product rule. Introduction to the derivative of e^x, ln x, sin x, cos x, and tan x
-
 Equation of a tangent line
cc
Equation of a tangent line
ccFinding the equation of the line tangent to f(x)=xe^x when x=1
Product and quotient rules
You can figure out the derivative of f(x). You're also good for g(x). But what about f(x) times g(x)? This is what the product rule is all about. This tutorial is all about the product rule. It also covers the quotient rule (which really is just a special case of the product rule).
-
 Implicit differentiation
cc
Implicit differentiation
cc -
 Showing explicit and implicit differentiation give same result
Showing explicit and implicit differentiation give same result
-
 Implicit derivative of (x-y)^2 = x + y + 1
Implicit derivative of (x-y)^2 = x + y + 1
-
 Implicit derivative of y = cos(5x - 3y)
cc
Implicit derivative of y = cos(5x - 3y)
cc -
 Implicit derivative of (x^2+y^2)^3 = 5x^2y^2
Implicit derivative of (x^2+y^2)^3 = 5x^2y^2
-
 Finding slope of tangent line with implicit differentiation
Finding slope of tangent line with implicit differentiation
-
 Implicit derivative of e^(xy^2) = x - y
Implicit derivative of e^(xy^2) = x - y
-
 Derivative of x^(x^x)
cc
Derivative of x^(x^x)
ccDerivative of x^(x^x)
Implicit differentiation
Like people, mathematical relations are not always explicit about their intentions. In this tutorial, we'll be able to take the derivative of one variable with respect to another even when they are implicitly defined (like "x^2 + y^2 = 1").
-
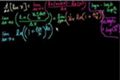 Proof: d/dx(ln x) = 1/x
cc
Proof: d/dx(ln x) = 1/x
ccTaking the derivative of ln x
-
 Proof: d/dx(e^x) = e^x
cc
Proof: d/dx(e^x) = e^x
ccProof that the derivative of e^x is e^x.
-
 Proofs of derivatives of ln(x) and e^x
cc
Proofs of derivatives of ln(x) and e^x
ccDoing both proofs in the same video to clarify any misconceptions that the original proof was "circular".
Proofs of derivatives of common functions
We told you about the derivatives of many functions, but you might want proof that what we told you is actually true. That's what this tutorial tries to do!
 Slope of a line secant to a curve
Slope of a line secant to a curve Slope of a secant line example 1
Slope of a secant line example 1 Slope of a secant line example 2
Slope of a secant line example 2 Approximating instantaneous rate of change word problem
Approximating instantaneous rate of change word problem Intuitively drawing the derivative of a function
Intuitively drawing the derivative of a function Intuitively drawing the antiderivative of a function
Intuitively drawing the antiderivative of a function