Khan Academy on a Stick : Sequences, series and function approximation

Khan Academy on a Stick

Calculus

Limits
Taking derivatives
Derivative applications
Indefinite and definite integrals
Solid of revolution
Sequences, series and function approximation
Double and triple integrals
Partial derivatives, gradient, divergence, curl
Line integrals and Green's theorem
Surface integrals and Stokes' theorem
Divergence theorem

Sequences and Series (part 1)
cc

Introduction to the arithmetic and geometric series
Sequences and series (part 2)
cc

Finding the sum of an infinite geometric series.

Sequences and series review

You want to learn about Maclaurin and Taylor series but are a little rough on your sequences and series. This tutorial will get you brushed up on the concepts, vocabulary and ideas behind sequences and series.

Maclaurin and Taylor Series Intuition
cc

Approximating a function at 0 using a polynomial
Cosine Taylor Series at 0 (Maclaurin)
cc

Approximating f(x)=cos x using a Maclauren Series (special case of a Taylor series at x=0)
Sine Taylor Series at 0 (Maclaurin)
cc

Sine Taylor Series at 0 (Maclaurin)
Taylor Series at 0 (Maclaurin) for e to the x
cc

Taylor Series at 0 (Maclaurin) for e to the x
Euler's Formula and Euler's Identity
cc

Rationale for Euler's Formula and Euler's Identity
Visualizing Taylor Series Approximations
cc

Using Wolfram Alpha to approximate sin(x)
Generalized Taylor Series Approximation
cc

Approximating a function around a non-zero x value
Visualizing Taylor Series for e^x
cc

Visualizing Taylor Series for e^x
Error or Remainder of a Taylor Polynomial Approximation
cc

Understanding the properties of the remainder or error function for an Nth degree Taylor approximation of a function
Proof: Bounding the Error or Remainder of a Taylor Polynomial Approximation
cc

Proof of the Lagrange Error Bound (the bound of the error)

Maclaurin and Taylor series

In this tutorial, we will learn to approximate differentiable functions with polynomials. Beyond just being super cool, this can be useful for approximating functions so that they are easier to calculate, differentiate or integrate. So whether you will have to write simulations or become a bond trader (bond traders use polynomial approximation to estimate changes in bond prices given interest rate changes and vice versa), this tutorial could be fun. If that isn't motivation enough, we also come up with one of the most epic and powerful conclusions in all of mathematics in this tutorial: Euler's identity.

Polynomial approximation of functions (part 1)
cc

Using a polynomial to approximate a function at f(0).
Polynomial approximation of functions (part 2)
cc

Approximating a function with a polynomial by making the derivatives equal at f(0) (Maclauren Series)
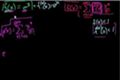Approximating functions with polynomials (part 3)
cc

A glimpse of the mystery of the Universe as we approximate e^x with an infinite series.
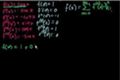Polynomial approximation of functions (part 4)
cc

Approximating cos x with a Maclaurin series.
Polynomial approximations of functions (part 5)
cc

MacLaurin representation of sin x
Polynomial approximation of functions (part 6)
cc

A pattern emerges!
Polynomial approximation of functions (part 7)
cc

The most amazing conclusion in mathematics!
Taylor Polynomials
cc

Approximating a function with a Taylor Polynomial

Sal's old Maclaurin and Taylor series tutorial

Everything in this tutorial is covered (with better resolution and handwriting) in the "other" Maclaurin and Taylor series tutorial, but this one has a bit of old-school charm so we are keeping it here for historical reasons.