Khan Academy on a Stick
Ratios and rational expressions
You have probably been wondering whether our powers of algebraic problem solving break down if we divide by the variable or we have entire expressions in denominator of a fraction. Well, they don't! In this topic, you'll learn how to interpret and manipulate algebraic ratios and rational expressions (when you have one algebraic expression divided by another)!
-
 The Golden Ratio
cc
The Golden Ratio
ccAn introduction to one of the most amazing ideas/numbers in mathematics
-
 Ratio problem with basic algebra (new HD)
cc
Ratio problem with basic algebra (new HD)
ccA slightly more involved ratio problem with algebra
-
 Writing proportions
cc
Writing proportions
ccSetting up proportions to solve a word problem
-
 More advanced ratio problem--with Algebra (HD version)
cc
More advanced ratio problem--with Algebra (HD version)
ccMore advance ratio problem with algebra.
-
 Advanced ratio problems
cc
Advanced ratio problems
ccMore advanced ratio problems
-
 Alternate Solution to Ratio Problem (HD Version)
cc
Alternate Solution to Ratio Problem (HD Version)
ccAn alternate solution to the advanced ratio problem in the last video.
-
 Another Take on the Rate Problem
cc
Another Take on the Rate Problem
ccAnother Take on the Rate Problem
-
 Find an Unknown in a Proportion
cc
Find an Unknown in a Proportion
cct2 Find an Unknown in a Proportion
-
 Find an Unknown in a Proportion 2
cc
Find an Unknown in a Proportion 2
cct2 Find an Unknown in a Proportion 2
-
 Proportions 2 exercise examples
Proportions 2 exercise examples
-
 Mountain height word problem
cc
Mountain height word problem
ccUsing some basic algebra to solve what looks like a hairy word problem that involves proportions.
Ratios with algebra
You remember a thing or two about ratios and proportions from you pre-algebra days. Well, how can we use these same ideas to solve problems in algebra. This tutorial re-introduces ratios in an algebraic context and helps us solve some awesome problems!
-
 Simplifying Rational Expressions Introduction
cc
Simplifying Rational Expressions Introduction
ccSimplifying Rational Expressions
-
 Simplifying Rational Expressions 1
cc
Simplifying Rational Expressions 1
ccU11_L1_T1_we1 Simplifying Rational Expressions 1
-
 Simplifying Rational Expressions 2
cc
Simplifying Rational Expressions 2
ccU11_L1_T1_we2 Simplifying Rational Expressions 2
-
 Simplifying Rational Expressions 3
cc
Simplifying Rational Expressions 3
ccU11_L1_T1_we3 Simplifying Rational Expressions 3
-
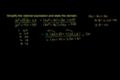 Simplifying Rational Expressions Example 2
Simplifying Rational Expressions Example 2
u15_L1_T1_we2 Simplifying Rational Expressions
Simplifying rational expressions
You get a rational expression when you divide one polynomial by another. If you have a good understanding of factoring quadratics, you'll be able to apply this skill here to help realize where a rational expression may not be defined and how we can go about simplifying it.
-
 Adding and Subtracting Rational Expressions
cc
Adding and Subtracting Rational Expressions
ccAdding and Subtracting Rational Expressions
-
 Adding and Subtracting Rational Expressions 2
cc
Adding and Subtracting Rational Expressions 2
ccU11_L1_T3_we2 Adding and Subtracting Rational Expressions 2
-
 Adding and Subtracting Rational Expressions 3
cc
Adding and Subtracting Rational Expressions 3
ccU11_L1_T3_we3 Adding and Subtracting Rational Expressions 3
-
 Subtracting Rational Expressions
cc
Subtracting Rational Expressions
ccSubtracting Rational Expressions
-
 Simplifying First for Subtracting Rational Expressions
cc
Simplifying First for Subtracting Rational Expressions
ccSimplifying First for Subtracting Rational Expressions
-
 Multiplying and Simplifying Rational Expressions
cc
Multiplying and Simplifying Rational Expressions
ccMultiplying and Simplifying Rational Expressions
-
 Multiplying and Dividing Rational Expressions 1
cc
Multiplying and Dividing Rational Expressions 1
ccMultiplying and Dividing Rational Expressions 1
-
 Multiplying and Dividing Rational Expressions 2
cc
Multiplying and Dividing Rational Expressions 2
ccMultiplying and Dividing Rational Expressions 2
-
 Multiplying and Dividing Rational Expressions 3
cc
Multiplying and Dividing Rational Expressions 3
ccMultiplying and Dividing Rational Expressions 3
-
 Rationalizing Denominators of Expressions
cc
Rationalizing Denominators of Expressions
ccRationalizing Denominators of Expressions
Rational expressions and equations
Have you ever wondered what would happen if you divide one polynomial by another? What if you set that equal to something else? Would it be as unbelievably epic as you suspect it would be? Well, rational expressions are just algebraic expressions formed by dividing one expression by another. We get a rational equation if we set that equal to something else. In this tutorial, we work through examples to understand and apply rational expressions and equations.
-
 Asymptotes of Rational Functions
cc
Asymptotes of Rational Functions
ccAsymptotes of Rational Functions
-
 Another Rational Function Graph Example
cc
Another Rational Function Graph Example
ccAnother Rational Function Graph Example
-
 A Third Example of Graphing a Rational Function
cc
A Third Example of Graphing a Rational Function
ccA Third Example of Graphing a Rational Function
Graphing rational functions
Rational functions are often not defined at certain points and have very interesting behavior has the input variable becomes very large in magnitude. This tutorial explores how to graph these functions, paying attention to these special features. We'll talk a lot about vertical and horizontal asymptotes.
-
 Partial Fraction Expansion 1
cc
Partial Fraction Expansion 1
ccIntroduction to partial fraction expansion
-
 Partial Fraction Expansion 2
cc
Partial Fraction Expansion 2
ccA more complex problem
-
 Partial Fraction Expansion 3
cc
Partial Fraction Expansion 3
ccDealing with repeated factors
Partial fraction expansion
If you add several rational expressions with lower degree denominator, you are likely to get a sum with a higher degree denominator (which is the least-common multiple of the lower-degree ones). This tutorial lets us think about going the other way--start with a rational expression with a higher degree denominator and break it up as the sum of simpler rational expressions.
-
 Ex 1 Multi step equation
Ex 1 Multi step equation
Turning a rational equation into a linear equation.
-
 Rational Equations
cc
Rational Equations
ccRational Equations
-
 Solving Rational Equations 1
cc
Solving Rational Equations 1
ccSolving Rational Equations 1
-
 Solving Rational Equations 2
cc
Solving Rational Equations 2
ccSolving Rational Equations 2
-
 Solving Rational Equations 3
cc
Solving Rational Equations 3
ccSolving Rational Equations 3
-
 Applying Rational Equations 1
cc
Applying Rational Equations 1
ccApplying Rational Equations 1
-
 Applying Rational Equations 2
cc
Applying Rational Equations 2
ccApplying Rational Equations 2
-
 Applying Rational Equations 3
cc
Applying Rational Equations 3
ccApplying Rational Equations 3
-
 Extraneous Solutions to Rational Equations
cc
Extraneous Solutions to Rational Equations
ccExtraneous Solutions to Rational Equations
-
 Rational Inequalities
cc
Rational Inequalities
ccTwo ways to solve a rational inequality (or an inequality involving a fractional expression)
-
 Rational Inequalities 2
cc
Rational Inequalities 2
ccSlightly harder rational inequality problem
Solving rational equations
The equations you are about to see are some of the hairiest in all of algebra. The key is to keep calm and don't let the rational equation be the boss of you.