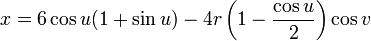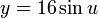Checked content

File:KleinBottle-01.png

KleinBottle-01.png ‎(240 × 300 pixels, file size: 64 KB, MIME type: image/png)
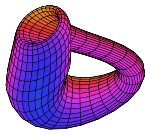
Mathematics icon This image was selected as picture of the month on the Mathematics Portal for November 2006

czech:Kleinova láhev je těleso,ve kterém nelze přejít přes okraj. Technicky vzato má jen jednu stranu. V knize Hravá matematika od Radka Chajdy jsem našel otázku: lze do Kleinovy láhve něco nalít? Ano lze do ní něco nalít a ještě není potřeba víčko.

Lukáš HOZDA 1.11.2009

Gnome-x-office-drawing.svg File:KleinBottle-01.svg is a vector version of this file.
It should be used in place of this raster image when superior.
File:KleinBottle-01.png Gnome-go-next.svg File:KleinBottle-01.svg

For more information about vector graphics, read about Commons transition to SVG.
There is also information about MediaWiki's support of SVG images.
New SVG image

Contents

See also

Image:Klein bottle.svg

Licensing

Public domain I, the copyright holder of this work, release this work into the public domain. This applies worldwide.
In some countries this may not be legally possible; if so:
I grant anyone the right to use this work for any purpose, without any conditions, unless such conditions are required by law.

Parameterization

This immersion of the Klein bottle into R3 is given by the following parameterization. Here the parameters u and v run from 0 to 2π and r is a fixed positive constant.

For 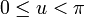0 \leq u < \pi:

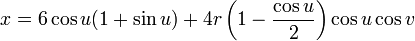
x = 6 \cos u(1 + \sin u) + 4r\left(1 - \frac{\cos u}{2}\right) \cos u \cos v
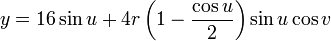
y = 16 \sin u + 4r\left(1 - \frac{\cos u}{2}\right) \sin u \cos v
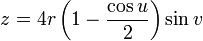
z = 4r\left(1 - \frac{\cos u}{2}\right) \sin v

For 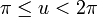\pi \leq u < 2\pi:

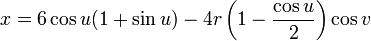
x = 6 \cos u(1 + \sin u) - 4r\left(1 - \frac{\cos u}{2}\right) \cos v
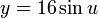
y = 16 \sin u\,
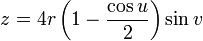
z = 4r\left(1 - \frac{\cos u}{2}\right) \sin v

Mathematica source 

KleinBottle[r_:1] =
 Function[{u, v},
   UnitStep[Sin[u]]
   {
       6 Cos[u](1 + Sin[u]) + 4r(1 - Cos[u]/2) Cos[u]Cos[v],
       16 Sin[u] + 4r(1 - Cos[u]/2) Sin[u]Cos[v],
       4r(1 - Cos[u]/2) Sin[v]
   }
   + (1 - UnitStep[Sin[u]])
   {
       6 Cos[u](1 + Sin[u]) - 4r(1 - Cos[u]/2) Cos[v],
       16 Sin[u],
       4r(1 - Cos[u]/2) Sin[v]
   }
 ]

 ParametricPlot3D[Evaluate[KleinBottle[][u, v]], {u, 0, 2Pi}, {v, 0, 2Pi},
   PlotPoints -> {50, 19}, Boxed -> False, Axes -> False,
   ViewPoint -> {0.454, -2.439, -2.301}]

The following pages on Schools Wikipedia link to this image (list may be incomplete):

I want to learn more...

Schools Wikipedia was launched to make learning available to everyone. SOS Children is famous for the love and shelter it brings to lone children, but we also support families in the areas around our Children's Villages, helping those who need us the most. You can help by sponsoring a child.
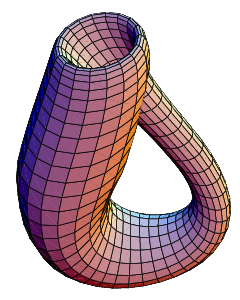
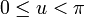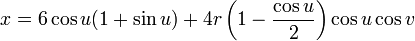
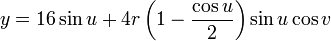
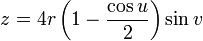
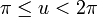