 |
This is a file from the Wikimedia Commons. Information from its description page there is shown below.
Commons is a freely licensed media file repository. You can help.
|
Summary
| Description |
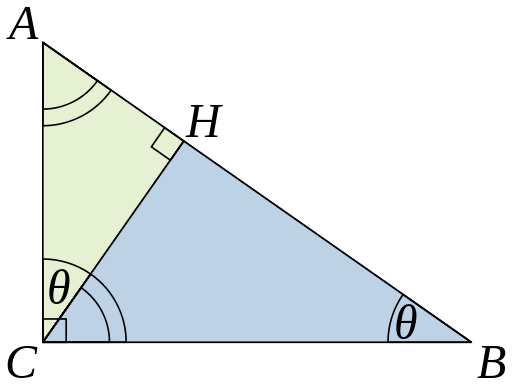
English: Simplified version of similar triangles proof for Pythagoras' theorem.
In triangle ACB, angle ACB is the right angle. CH is a perpendicular on hypotenuse AB of triangle ACB.
In triangle AHC and triangle ACB, ∠AHC=∠ACB as each is a right angle. ∠HAC=∠CAB as they are common angles at vertex A. Thus triangle AHC is similar to triangle ACB by AA test.
Thus, 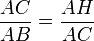 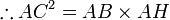
In triangle BHC and triangle ACB, ∠BHC=∠ACB as each is a right angle. ∠HBC=∠CBA as they are common angles at vertex B. Thus triangle BHC is similar to triangle BCA by AA test.
Thus, 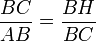 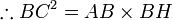
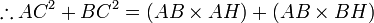
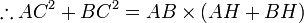
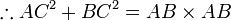
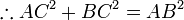 which is the Pythagoras theorem.
|
| Date |
2012-05-15 10:08 (UTC) |
| Source |
This file was derived from:
Reference:
- ↑ (2011) GEOMETRY Standard X, Secretary, Maharashtra State Board of Secondary and Higher Secondary Education, Pune-411 004, pp. 22, 23
|
| Author |
- derivative work: Gauravjuvekar
- derivative work: Gauravjuvekar
|
|
|
 ✓ The source code of this SVG is valid. ✓ The source code of this SVG is valid.
|
|
This vector image was created with Inkscape. |
|
 |
This is a retouched picture, which means that it has been digitally altered from its original version. Modifications: Simplified and removed lower-case notations and related elements per some comments at Wikipedia:Featured picture candidates/Pythagoras similar triangles proof. The original can be viewed here: Pythagoras_similar_triangles.svg. Modifications made by Gauravjuvekar.
|
Licensing
| Public domainPublic domainfalsefalse |
 |
This image of simple geometry is ineligible for copyright and therefore in the public domain, because it consists entirely of information that is common property and contains no original authorship.
|
|
Assessment
 |
Quality image
This image has been assessed using the Quality image guidelines and is considered a Quality image.
|
File usage
The following pages on Schools Wikipedia link to this image (list may be incomplete):
This file contains additional information, probably added from the digital camera or scanner used to create or digitize it. If the file has been modified from its original state, some details may not fully reflect the modified file.
Wikipedia for Schools is one of SOS Childrens Villages' many educational projects. Our 500 Children's Villages provide a home for thousands of vulnerable children. Beyond our Villages, we support communities, helping local people establish better schools and delivering effective medical care to vulnerable children. Sponsoring a child is a great way to help children who need your support.

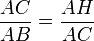
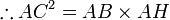
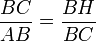
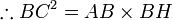
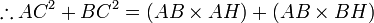
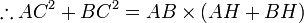
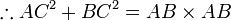
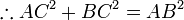 which is the Pythagoras theorem.
which is the Pythagoras theorem.


